Wielding (quantum) fields!

Quantum field theory takes an infinite number of field configurations and add them up with the proper weighting to come to a single conclusion. The Standard Model is one well-known example, but this could be much, much more useful. For example, we could predict readings on compasses – something we can’t do right now – at different altitudes as climbers go up mountains. It might sound simple, but gravity, and all the infinite number of fields generated by planet earth, are actually incredibly complicated.

 

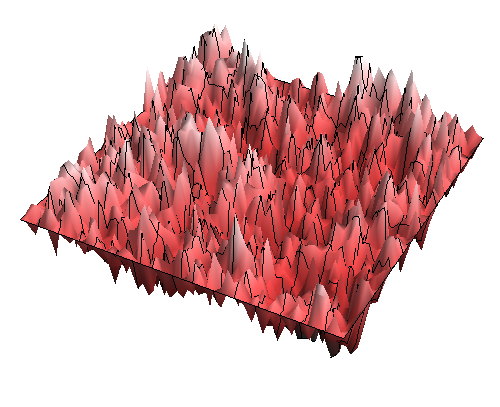Gaussian free field model by Samuelswatson via Wikipedia.

This process of adding up infinite fields is known as a Feynman path integral, where “path” tells us it is route dependent, i.e. the result depends on how you get there, and “integral” describes a calculation of the data area or volume. The path integral should take infinitely long, but mathematicians have now managed to solve the Liouville field, which gather an infinite number of space-times together to model gravity on a two dimensional surface^[1].

Richard Feynman developed a limited model in the 1940s, but it only works for free fields, which are non-interacting. More complex fields can be solved through “fudges” that involve pretending they’re free fields and then adding small perturbations. Sadly, this can’t work for the Liouville field, because it interacts with itself too strongly.

So what did the mathematicians do?

They solved it using a method where three measurements are chosen randomly, and the correlation functions between them are calculated; this result is then used to construct a four-point function, which constructs a five-point function, and so on. This can solve the field, but only if you guess the right starting measurements – otherwise it tends to go a bit crazy.

Actually, the mathematicians solved the Liouville field by chance – by simply guessing the right starting measurements. At least, to begin with.

But then they thought of something better.

They used a Gaussian free field model, which fluctuates, but not as much as a Liouville field, and allowed them to calculate sensible averages for three, four, five, and, eventually, infinite measurements. And, magically, this came up with the same equations as physics – equations that hadn’t been explained before, but work to describe reality. This means the solution could provide insight into how the physical world works and its mathematical origins, as well as provide us with working predictive tools.

There is still no general way to meaningfully average an infinite number of objects. And, indeed, solving this is one of the Millennium Problems, worth £1m. However, the results for the Liouville field problem could work in other two-dimensional environments.

References
why don't all references have links?

[1] Polyakov, Alexander M. Quantum geometry of bosonic strings. Physics Letters B 103.3 (1981): 207-210. doi: 10.1016/0370-2693(81)90743-7.